Degenerate Dot Product Attention
Motivation
In a deep learning course that I’m taking this semester, we were recently asked to implement multi-headed dot product attention in a causal gpt-like transformer. I ran into an interesting pitfall that I wanted to share, so that others can avoid making the same mistake, while also digging deeper into the attention mechanism. If you want to skip the background and jump straight into the explanation, click here.
Background
For a more comprehensive review of the transformer architecture and dot-product attention, please refer to this great resource written by Jay Alammar: The Illustrated Transformer. If you are familiar with this material, feel free to skip this section.
Here is a quick refresher on the attention mechanism:
Given a sequence of token embeddings \(h \in \mathbb{R}^{L \times d_h}\), we first compute the query, key, and value matrices \(Q, K, V \in \mathbb{R}^{L \times d_k}\) by multiplying the embeddings by learned weight matrices \(W_Q, W_K, W_V \in \mathbb{R}^{d_h \times d_k}\):
\[Q = hW_Q, \quad K = hW_K, \quad V = hW_V\]For this analysis, I will assume that we use a single head of attention, so \(d_k = d_h\). Next, the raw attention scores \(A \in \mathbb{R}^{L \times L}\) is computed as follows:
\[A_{\text{raw}} = \frac{QK^T}{\sqrt{d_k}}\]\(A\) is an \(L \times L\) matrix where the row dimension corresponds to the queries and the column dimension corresponds to the keys. Thus, we can think of the entry at \((i,j)\) as the amount of attention that the \(i^{th}\) token should pay to the \(j^{th}\) token, when attempting to predict the next token in the sequence. Obviously, we don’t want the model to cheat by looking at future tokens, so we apply a lower triangular mask \(M\) to \(A\) that zeroes out the entries above the diagonal.

Finally, we apply a row-wise softmax to normalize the attention scores for each query. This softmax operation is performed on the rows (query) dimension, since we want to normalize the attention scores of each query \(i\) across the keys \(j<i\) that come before it. This is the key insight that enables the transformer to be causal, since the model can only attend to tokens that come before it in the sequence. We obtain the next token embedding \(h_{i+1}\) by multiplying the softmaxed attention scores \(A_{\text{final}}\) by the value matrix \(V\).
\[\begin{split} A_{\text{final}} &= \text{softmax}(A_{\text{raw}}) \\ h_{i+1} &= A_{\text{final}}V \end{split}\]Degenerate Attention
Now that we have reviewed the attention mechanism, let’s look at the problem that I ran into. Instead of performing softmax over the query (row) dimension of the \(L \times L\) self-attention matrix, I instead performed softmax over the key (column) dimension. This is a subtle mistake that is easy to miss, since the softmax operation is symmetric and the row and column dimensions are interchangeable.
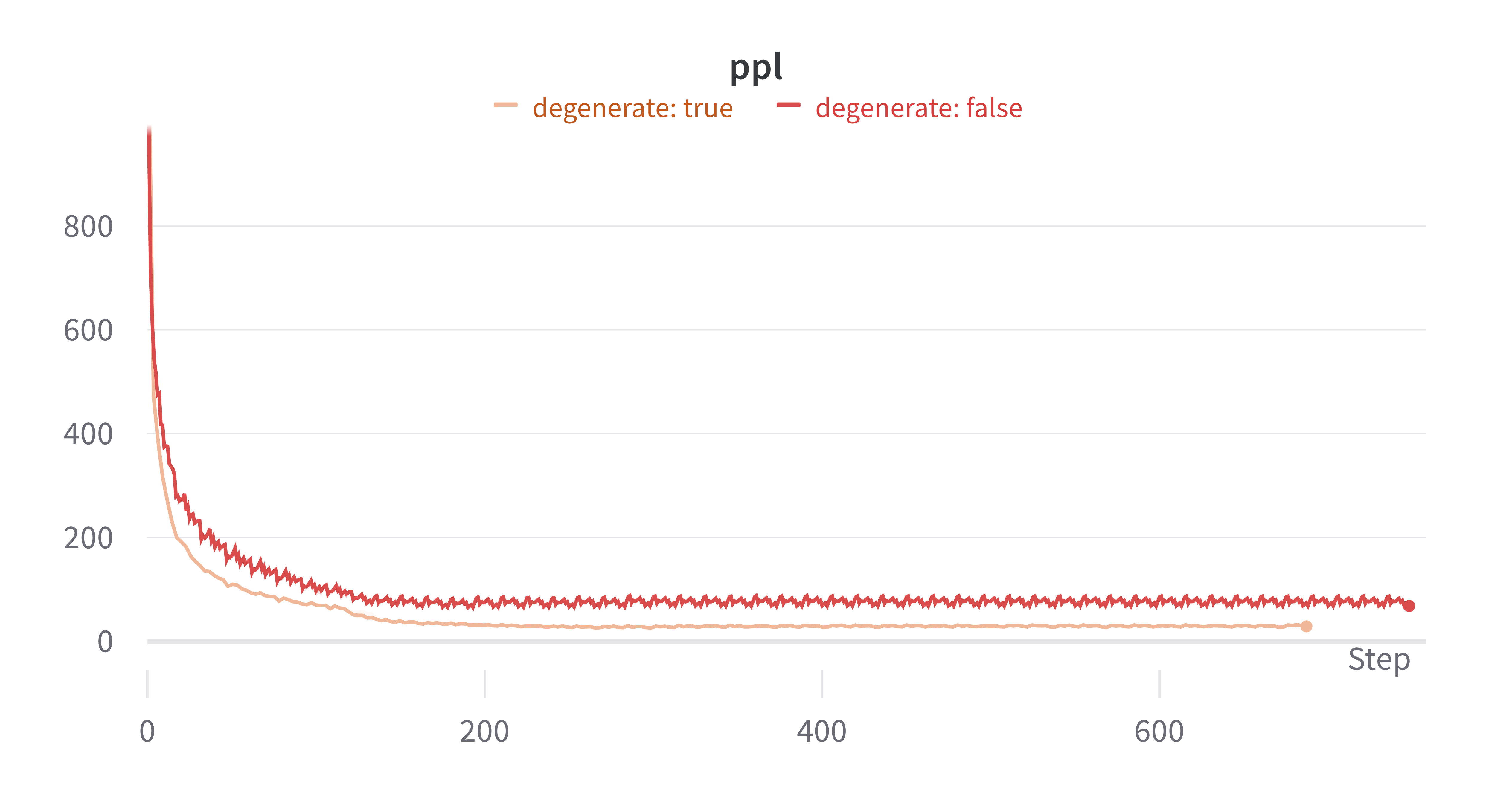
After training my model for a few epochs on the wikitext-2 dataset, I noticed that my model was achieving state of the art perplexity on the validation set, and showed no signs of overfitting. Here are some plots of the training and validation perplexity over time. I knew that something was wrong, since the perplexity was too good to be true, so I decided to investigate further. I named this phenomenon degenerate attention, and ran some comparisons with the correct implementation of softmax over the row dimension.

Initially, I was extremely perplexed since the attention matrix in degenerate attention was still lower triangular, which prevented tokens from directly attending to future tokens. So, to elucidate the situation, I decided to generate some text using the degenerate transformer, and visualize the attention scores between layers using the bertviz package.
As expected, text generated from the degenerate transformer was complete gibberish, since the model was able to cheat by attending to future tokens. Here is an example passage:
”,,,,,,,,,, in and in, in’from, from some in available available available playing some focused close in added interested re added some far re Al some self individual focused returning available far some some added Al re re some far serious re re half re construction re Cor self re forced re ill Rox beginning eight Villa necessary air Cal Secretary fast far re increased far re far Abu operating Villa re scored Less some re re re free re re concrete international re concrete some re re”
However, I realized that the softmax operation was still allowing information to leak from future tokens to past tokens. This is because the softmax operation is performed on the column dimension, so the attention scores of each key \(j\) are normalized across the queries \(i>j\) that come after it. This is a subtle but important difference,
Further, when we look at the top-k output logits from the classifier head, we see that the degenerate transformer gives extremely high probabilities to the correct token, but the next highest probability tokens are incoherent with respect to the sentence. Here is an example:
| Original sentence | “I went to the cinema where I saw a movie” |
| Top 1 prediction | “I went to the cinema where I saw a movie” |
| Top 2 prediction | “I resigned by a trust when appeared for the Year” |
| Top 3 prediction | “I Squadron of The Argentina after Y drew since to” |
Finally, here are the attention score visualizations obtained via bertviz. As expected, the model attends much more to recent tokens given that the softmax forces each column of the attention matrix to sum to 1.
Explanation
These were all clear signs that there was data leakage allowing the degenerate model to see future tokens, which was making the next word prediction task trivial. However, I was still confused as to why the model was able to achieve such good performance. After some thought, I finally figured out where the issue was. The key is that although the self-attention matrix remains lower triangular, softmaxing over the column space (queries dimension) introduces a source of correlation between the independent rows that the model can exploit. By tuning the raw attention scores, the model “hacks” the softmax operation by using it to pass information from future tokens to past tokens. Let’s look at this two step process in more detail:
- Each token \(i\) in the sequence computes the pre-softmax attention values over the previous tokens \(j\leq i\) in the input sequence.
- Degenerate attention normalizes the attention scores column-wise, across each query token, which introduces a source of correlation among the attention scores of each row (key)
Thus, the model is smart enough to figure out a way to tune the pre-softmax attention values in step 1 so that information is then passed from future tokens to past tokens in step 2 of the column-wise softmax. Compare this to normal attention where there is no way for the rows in the attention matrix to influence each other since the softmax is performed on the row dimension.
Conclusion
Although this blog post was a bit of a rant, I hope that it was helpful for those who are trying to understand the attention mechanism in transformers. I also hope that it will help others avoid making the same mistake that I did, while provide an important reminder that neural networks will always take the path of least resistance. Finally, I’d like to thank my dear friend Thomas Jiralerspong for helping me debug this issue and providing feedback on this blog post.
The code for this project can be found here, if you want to try degenerate attention yourself for some reason…